What is quantum metrology?
Quantum metrology studies how quantum effects—such as superposition, entanglement, and squeezing—can be used to measure physical parameters with higher precision than is possible using classical strategies.
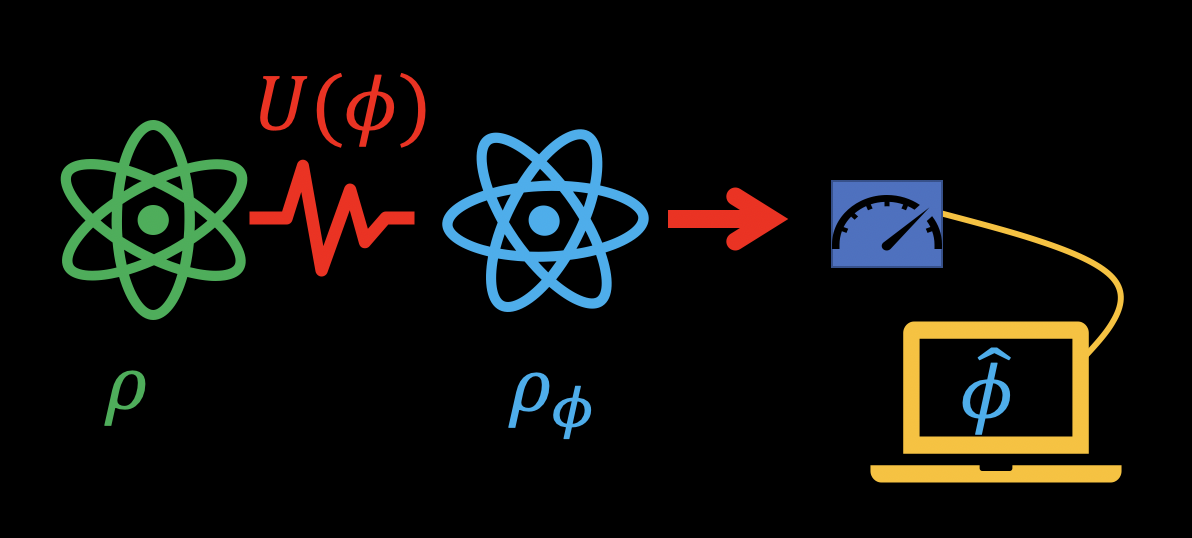
Typical sensing workflow
In our work, a sensing protocol is treated as a controlled quantum process rather than a fixed experiment.
Core methods
- Quantum Fisher information (QFI) and quantum Fisher information matrix (QFIM)
- Time-dependent and optimal control of probe dynamics
- Noise modeling and robustness analysis
- Variational and learning-based optimization of states and measurements
Research topics
Time-dependent sensing
We design control schedules that maximize information gain within finite sensing times.
Networked quantum sensors
Distributed sensing using multiple nodes, optimized for scalability and realistic noise.
Multiphase and multiparameter estimation
Understanding trade-offs, compatibility conditions, and joint estimation limits.
Robust measurement design
Constructing POVMs that remain near-optimal under imperfect calibration and readout.
Selected results
- Squeezing-induced quantum-enhanced multiphase estimation
- Time-normalized quantum Fisher information
- Noise-robust performance of networked quantum sensors
Why it matters
Precision measurement underpins modern science and technology. By explicitly accounting for noise, control, and finite resources, our work helps bridge the gap between fundamental limits and deployable quantum sensors.